 ...Wie geil ist das denn?
...Wie geil ist das denn?
Als erstes will ich hier mal - ja so einen bösen "externen Link" matplotlib.org setzen. Da können sie mal so einen Tag schauen und spielen... aber dann ggf. wieder zurück kommen..😔Wie man sieht gibt es da wahnsinnige Ausgaben zu sehen. Ich will hier mal ein Beispiel hervorheben - einfach weil mich der Gedanke einfach umgehauen hätte soetwas so einfach vor 30 Jahren zur Verfügung gehabt hätte.
Das Doppelpendel
Für alle die in der Schule Physik nach der 5. Klasse mental abgewählt haben - oder für Freunde der "Tagesschau in einfacher Sprache" - so ein "Doppelpendel" ist ein Pendel, an dessen Ende ein weiteres Pendel hängt. Das "normale" Pendel ist immer das Paradebeispiel dafür, wie schön übersichtlich und auch für Schüler gut berechenbar Lageenergie (od. Potentielle Energie) kinetische Energie umgewandelt wird. Ich formulier das mal flapsig: 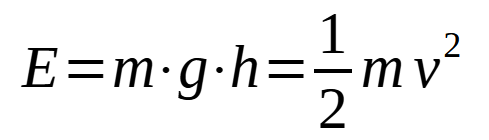
Ganz grob m ist die Masse des idealisierten Pendels vereinigt in einer Punktmasse am schwingenden unteren Ende. h seine der Höhenunterschied zwischen dem Punkt der höchsten Auslenkung und dem tiefsten Punkt der Pendelwegs.
Aus täglicher Anschauung weiß man (hoffentlich), dass so eine Pendelgewicht (oder ein Mensch auf einer Schaukel) am Tiefsten Punkt am schnellsten ist (v sei eben diese Geschwindigkeit ) und am höchsten Punkt die Richtung wechselt - der Betrag der Geschwindigkeit einen Moment 0 ist. Wegen der Energieerhaltung ergibt sich so zu jedem Zeitpunkt, Höhe und Geschwindigkeit... äh mal so grob. Die Bewegung ist aber nahezu einschläfernd langweilig...
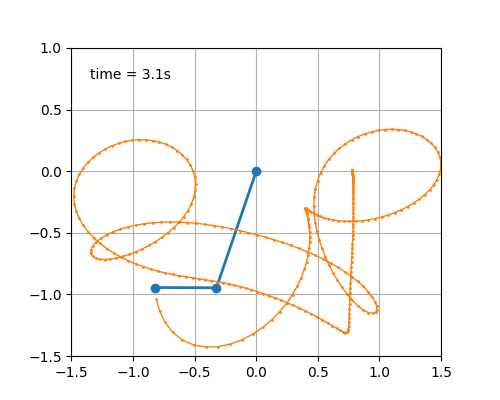
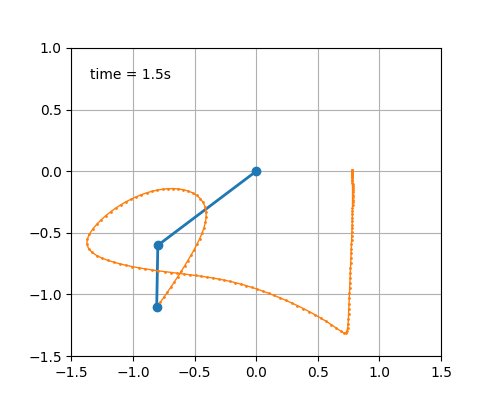
Richtig Leben in die Bude kommt wenn man eben ein zweites Pendel an das erste Pendel anhängt.
Für die meisten erstmaligen Beobachter einigermaßen überraschend, "zappelt" ein solches Doppelpendel recht aufgeregt und 'unvorhersehbar' durch die Gegend. Das "blaue Gestänge" ist hier das Pendel - das "Orangene" der Weg des unteren Pendelgewichts.
Ich habe hier ein wenig experimentiert und zwei verschiedene Verhältnisse der Pendelgewichte 1 + 2 gewählt. Nu raten sie welches welches ist...
Es wird deshalb gerne zur Demonstration chaotischer Prozesse
hergenommen. Ganz gut erklärt z.B. auch auf Wikipedia
Ich will hier jetzt niemanden mit Physik, noch Mathe quälen - aber wie nützlich numpy und matplotlib sind, erkennt derjenige, der es braucht ganz einfach an den Verlinkten Beispielen. Dort gibt's auch für 'alle anderen' bunte und beeindruckend dreidimensionale Beispiele😁
Einen kurzen Blick - wie einfach der Umgang mit diesem Modul - will ich aber doch noch sozusagen "Hallo Welt" Beispiel hier darstellen.
Auf Probleme wo dieses hilfreich sein könnte, trifft auch, wer sich sonst erfolgreich von Mathe & Co fern hält. Mal eben Werte in ein Koordinatensystem eintragen kann jedem mal passieren. Hier übrigens eine konkrete Anwendung: Weg nachzeichnen